证券基础知识(34)
lucy22668 2024年02月23日 星期五 上午 7:31
今天居然在最后尾巴翘起来了,A股真是让人又爱又恨。这个时候,就别乱动了,已经差不多到底部了。
继续学习吧。
一、两个资产收益
首先,来看看两种资产,当明白两种资产之间的关系的时候,很容易就把它扩展到n种资产。现在假设要投资两种资产,这两种资产的相关系数是p,投资比例分别为w1和w2,满足w1+w2=1,组成的新的组合我们称之为P。问题是:新的组合P,所具有的期望收益率和风险是多少呢?先看看收益怎么算,为了计算组合P的收益率,需要知道组合P的期初价值和1期期末价值是多少?假设这两个资产期初价格分别是P0和Q0。过了1年以后资产价格分别变成了P1和Q1。现在假设期初投资金额为L,分别去购买第1个资产和第2个资产,其中有w1xL投资在第1个资产上,w2xL投资在第2个资产上。所以组合P期初价值就是L。到了期末,第1类资产期末的价值变成了(w1xL/P0)xP1,第2类资产期末的价值就变成了(w2xL/Q0)xQ1。所以第1期期末资产组合P的价值就变成了:(w1xL/P0)xP1+(w2xL/Q0)xQ1
所以,任何一个新的组合,其收益率就等于组成这个组合的资产收益率的加权平均,也就是: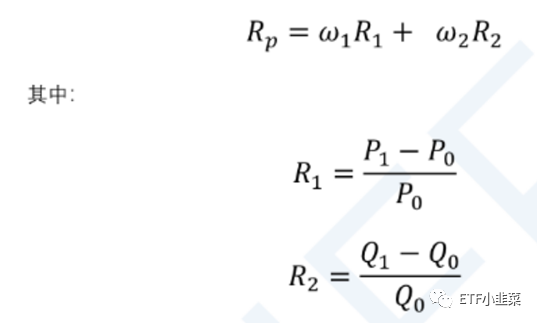
二、两种资产的风险
利用概率论的知识,新的组合方差等于这个组合资产的方差乘以各自的权重的平方,再加上两两之间的协方差乘以相应的权重。也就是: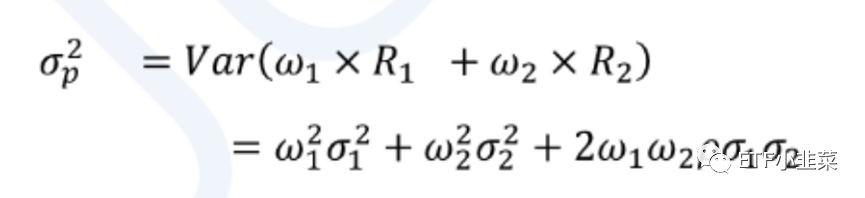
三、无风险资产+风险资产收益率和风险的关系
两个资产组成的组合的收益率和风险标准差都知道以后,就可以分析不同的资产组合权重下,资产组合的收益和风险之间的关系。从最简单的例子开始。假设这两种资产里面第1个资产是无风险资产,第2个资产是有风险资产。这意味着这两种资产之间的相关系数等于零,其中第1个资产的风险σ1=0,因此组合的标准差就等于第2个资产的权重的乘以第2个资产的标准差。在横轴是风险(标准差),纵轴是期望收益率二维坐标系下,不同组合权重下的资产组合,其收益和风险之间组成的点的轨迹如下图: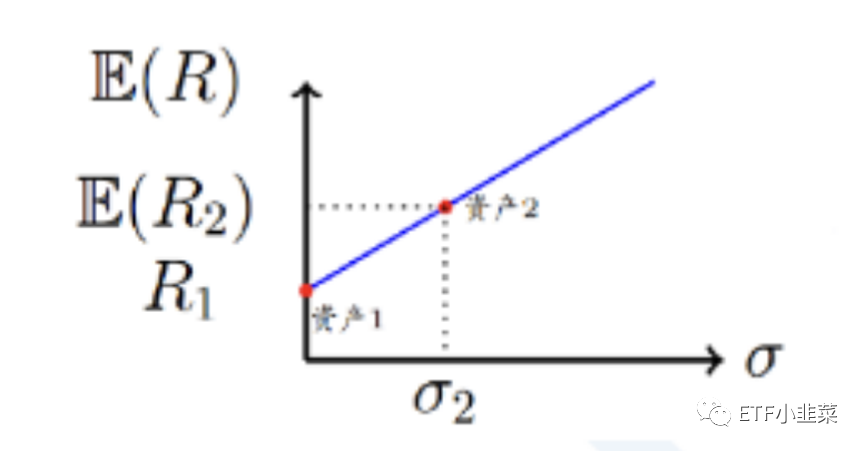

 本文内容来自网络,仅供学习、参考、了解,不作为投资建议。股市有风险,投资需谨慎!
本文内容来自网络,仅供学习、参考、了解,不作为投资建议。股市有风险,投资需谨慎!